Раздел 2: Анализ пикового соответствия спектра комбинационного рассеяния

В этом разделе мы расскажем о подгонке пиков, что важно для количественной оценки спектров комбинационного рассеяния. Сначала мы объясним, как выбрать функцию формы пика, а затем объясним метод количественного анализа интенсивности пика, положения пика и полуширины.

Процесс подбора пика состоит в том, чтобы найти форму пика, при которой ошибка была наименьшей для измеренного пика. Для этого сначала нужно выбрать базовую функцию формы пика. Типичные функции формы пика включают функцию Лоренца и функцию Гаусса. Соответствующие формулы показаны ниже. Вы можете видеть, что в этих уравнениях форма пика определяется путем определения трех параметров: интенсивности (A), положения (x0) и ширины (w). Сравнивая формы пиков в одинаковых условиях, вы можете увидеть следующие различия в форме пиков.

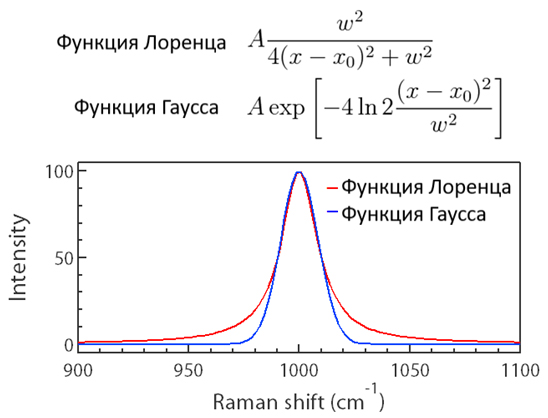
Сравнение функции Лоренца и Гаусса (число центральной волны 1000 см^-1, полная ширина на половине максимума 20 см^-1, интенсивность 100).

Форма спектра комбинационного рассеяния в идеале является функцией Лоренца, но когда образец измерения является аморфным, режим колебаний часто распространяется как функция Гаусса. Следовательно, необходимо выбрать соответствующую форму пика в зависимости от материала и его состояния. Функция Фойгта, полученная путем свертки функции Лоренца и функции Гаусса, также используется для подгонки пиков. Функция Фойгта используется, когда форма пика не является ни функцией Лоренца, ни функцией Гаусса, а находится между ними.

Интенсивность пиков могут быть легко рассчитаны из спектра, когда нет перекрывающихся пиков, но, если пики перекрываются, требуется анализ подгонки пиков. Ниже мы представляем пример оценки отношения интенсивности пиков, чтобы оценить ориентацию растянутой пленки Ag-отслаивания.

В спектре ниже будут оценены пики при 1059 см^-1 и 1126 см^-1, но между ними находиться еще пик с небольшой шириной. Следовательно, надежный метод оценки заключается в получении интенсивности каждого пика в виде суперпозиции трех пиков. На рисунке ниже сплошная линия - необработанные данные, пунктирная линия - результат подгонки, который получил хорошую сходимость с тремя пиками (функция Лоренца). Соответствующие пиковые интенсивности были такими, как показано на фигуре, и в результате отношения пиковых интенсивностей I(1126)/I(1059) должны были составлять 1,96 и 1,54 соответственно.

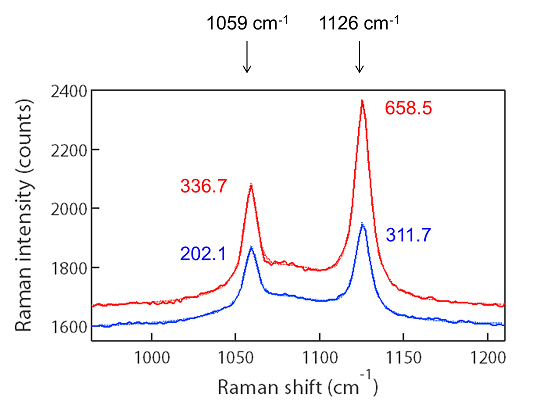
Оценка подгонки пиков.

При оценке напряжения, создаваемого в материале, оценивают величину сдвига пика относительно положения пика в отсутствие напряжения. Поскольку величина пикового сдвига имеет линейную зависимость от напряжения независимо от материала, таких как полупроводники и полимеры, для точного получения величины пикового сдвига используется подгонка пика. Ниже приведен пример оценки напряжений кремниевой подложки. График представляет собой спектр комбинационного рассеяния в свободной от напряжения части и части, где генерируются растягивающие и сжимающие напряжения. Кажется, что нет никакого изменения в положении пика, когда вы смотрите только на положение вершины пика, но положения пика немного отличаются. Когда это было вычислено путем подгонки пика, соответствующие положения пиков были рассчитаны как 519,94 см^-1, 520,00 см^-1, 520,09 см^-1.

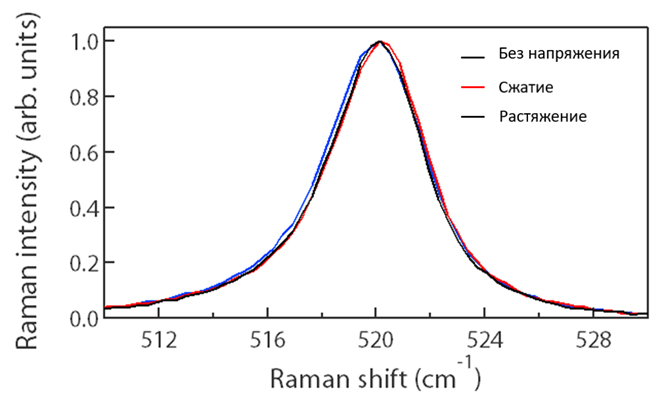
Оценка положения после подгонки пиков.

Полная ширина на половине максимума (FWHM) является показателем, который используется при оценке кристалличности полимеров и полупроводников. Например, известно, что для полимеров полуширина коррелирует с плотностью. Ниже приведен пример оценки кристалличности ПЭТ. Известно, что кристалличность ПЭТ различается в зависимости от положения ПЭТ-бутылки, и эти изменения можно оценить по пику при 1730 см-1, который соотноситься со связью С=О. Для пиков на рисунке ниже полная ширина на половине максимума (FWHM) была определена как 22,4 см^-1, 24,9 см^-1, 26,6 см^-1. Кроме того, во время пиковой подгонки материал был аморфным, поэтому подгонка проводилась с использованием гауссовой функции.

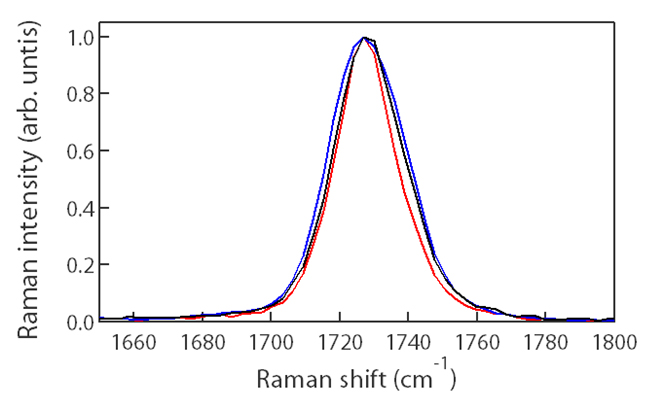
Оценка FWHM путем подгонки пиков.